In search of Hidden Conservation Laws
Numerical experiments are just what their name implies: experiments. In describing and evaluating them, one should enter the state of mind of the experimental physicist, rather then that of the mathematician. Numerical experiments cannot be used to prove theorems; but, from the physicist's point of view, they do often provide convincing evidence for the existence of a phenomenon. We will therefore follow an informal, descriptive and non-rigorous approach. Briefly stated, our aim will be to understand the fundamental properties of dynamical systems rather then to prove them.
In physics, questions about motion are addressed with the help of integrals of motion - numerical quantities which remain constant throughout the trajectory of the moving body. The conservation laws for this quantities pose restrictions on the achievable trajectories of the moving body. Given the space of all possible trajectories, each constant of motion acts as sieve, letting through trajectories that abide by the conservation law and getting rid of the ones that violate it.
In mathematical terms, for a given system with $s$ degrees of freedom, we are guaranteed $2s-1$ independent integrals of motion. See Landau and Lifschitz, Mechanics, § 6. Assuming a Hamiltonian system, the integrals of motion take the form of some function: $$I_j\left(q_1, q_2, \ldots, q_s; p_1, p_2, \ldots, p_s\right)$$ such that: $$I_j = C_j$$ for some constants $C_1, C_2, \ldots, C_{2s-1}$ and coordinates $q_i$ with conjugate momenta $p_i$. Each equation represents a hypersurface in the phase space, and the trajectory is the intersection of the $2s-1$ hypersurfaces. However, not all integrals of motion are equal. Some are more helpful then other when it comes to filtering the possible trajectories - just like a finer sieve is more effective then a coarse one. In essence, some equalities $I_j = C_j$ may cover the whole phase space and, thus, not provide any new information about the trajectory. Those are often termed nonisolatinig, while the useful ones - isolating.
Consider, for example, a planet orbiting a star. In cylyndircal coordinates $r$, $\theta$, $z$, the Hamiltonian of the system is: $$H = T + V = \frac{1}{2m}\left[ p_r^2 + \frac{p_{\theta}^2}{r^2} + p_z^2 \right] + V(r, z)$$ where $V(r, z)$ is axisymmetric central potential. In this case, while we are given 5 integrals of motion, only 2 are known to be isolating, namely the total energy $E = H$ and the z-component of the angular momentum $L_z = p_\theta$.
For a long time, only those two integrals where considered to be isolating, on the ground that no third integral can be expressed analytically - like the energy or angular momentum. On the other hand, experimental work has given evidence for a third isolating integral governing the motion of celestial bodies. Most notably, the faulty belief implies equal dispersion of velocities in the radial and perpendicular direction of the galactic plane, whereas the observed dispersions have approximately 2:1 ratio. See Sussman and Wisdom, Structure and Interpretation of Classical Mechanics, § 3.6.3 for a good discussion on the topic. Attempts were made to prove theoretically the existence of a third integral. Most notably, Contopoulos 1963, "A Classification of the Integrals of Motion." Here I follow the work of Hénon and Heiles Hénon and Heiles 1964, "The Applicability of the Third Integral Of Motion: Some Numerical Experiments" and adopt a numerical approach to the problem of disovering hidden isolating integrals of motion. First, investigating the Hénon-Heiles system and, afterwards, applying the same techniques to the infamous Three Body Problem.
Rather then studying the particulars of galactic dynamics, we abstract the dynamical problem by adopting the system of Hénon and Heiles - a two-degree-of-freedom system with a particularly simple potential energy so that the dynamics would be clear and the calculations uncluttered. The Hénon-Heiles Hamiltonian is: Contours of the Hénon-Heiles potential energy on the $(x, y)$ plane. The contours shown, from inside out, are for the potential energies $1/100$, $1/40$, $1/20$, $1/12$, $1/8$, $1/6$. $$H(t; x, y; p_x, p_y) = \frac{1}{2} (p_x^2 + p_y^2) + V(x, y)$$ with potential: $$V(x, y) = \frac{1}{2} (x^2 + y^2) + x^2 y - \frac{1}{3} y^3$$ At small values of the potential energy, the contours are approximately circular; as the value of the potential energy approaches $1/6$ the contours become triangular. For larger values, the contours open up to infinity.
The Hamiltonian does not have explicit dependece on time, therefore, a known isolating integral is the total energy. In this case, this is the only known such quantity. Given the restrictions implied by the energy conservation law, we can see that the total energy should satisfy: $$E = \frac{1}{2} (p_x^2 + p_y^2) + V(x, y) \geq V(x, y)$$ since $p_x^2$ and $p_y^2$ are non-negative. We can plot the zero-velocity curve described by the points $(x, y)$ which satisfy $E = V(x, y)$, for a given energy $E$. This curve encloses the region accessible to the moving body. As first step to get us familiar with the system, let us plot some trajectories for the energy level $E = 1/8$.
It is clear that variously different trajectories are possible. There are some that circulate in beautiful patterns around the triangular potential bowl, or oscillate between edges of the zero-velocity curve. Others, however, are more chaotic, without any regular patterns. The question facing us is - are there conservation laws (isolating integrals) other then the total energy in this system? A priori, there appear to be two possibilities: either there are hidden conservation laws or there are not. If there are not, we would expect that at some point in the future (it may take a while) all the space that is consistent with conservation of energy will be explored (as it looks like in the right-most trajectory above). On the other hand, if there indeed are hidden conservation laws, for some initial positions in the phase-space only subset of the space would be accessible. In the few experiments we have done so far (the first two trajectories above) we have already seen some "regularity" that "constraints" the motion of the body. These constraints imply the existence of a hidden conservation law. In what follows, we attempt to categorize those regularities and get an intuition for when they occur.
Paradoxically, it turns out that by throwing out most of the calculated information about a trajectory we gain essentially new information about the qualitative characteristics of the trajectory. A powerfull tool that extracts the essence by throwing away information is a technique known as surface of section or Poincaré section. See Poincaré 1892, "Les Méthodes Nouvelles de la Mécanique Céleste." In our case, we generate the surface of section by recording and plotting $p_y$ versus $y$ whenever $x=0$.
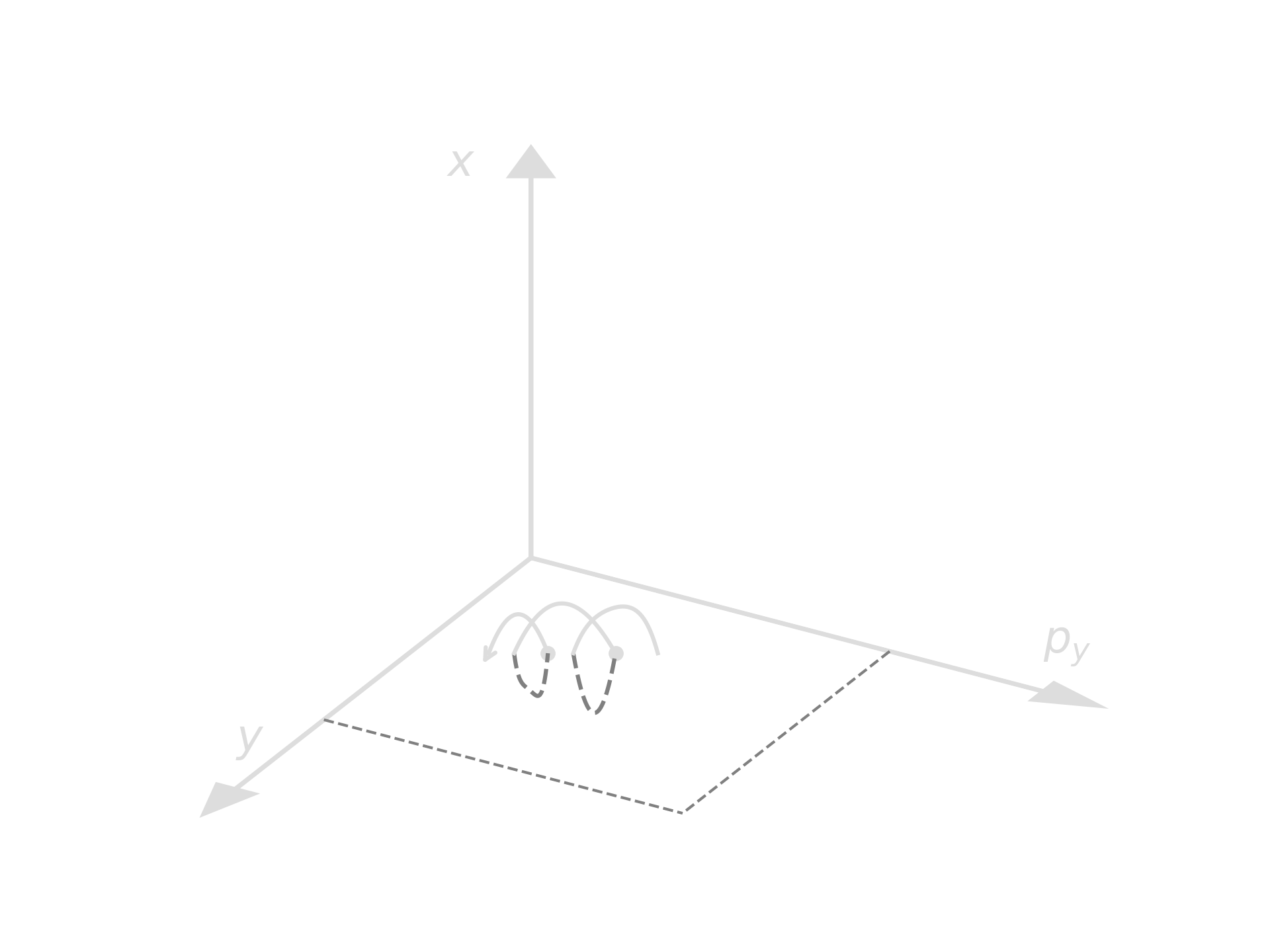
For a given energy value $E$ and coordinates $(y, p_y)$ on the section $x=0$ we can recover $p_x$ up to a sign. By focusing only on intersections which cross the $y-p_y$ plane from below (i.e. positive $p_x$) we establish a one-to-one correspondence between a section point and a trajectory. Therefore, for each section point there is a unique trajectory that passes through it.
On the section, the energy is $$E = H(t; 0, y; p_x, p_y) = \frac{1}{2}(p_x^2 + p_y^2) + V(0, y)$$ since $p_x^2$ is positive, the points on the section must satisfy $$E \geq \frac{1}{2} p_y^2 + V(x=0, y)$$ Thus, if there is no other conserved quantity, we expect the points on the section to eventually fill the region consistent with the above inequality.
On the other hand, suppose there exists a hidden isolating integral of motion $I(x, y; p_x, p_y) = C$. Conservation of energy allows us to get an expression relating $y$, $p_x$ and $p_y$ on the section ($x=0$): $$f(y, p_x, p_y) = E$$ Thus, we can express $p_x$ in terms of $y$ and $p_y$: $$p_x = g(y, p_y)$$ Utilizing our hypothesized isolating integral $I$, we get an exact relation between $y$ and $p_y$ on the section: $$I(x=0, y; g(y, p_y), p_y) = C$$ Thus, if there is a hidden isolating integral of motion, we expect the points on the section to fall on a curve.
To summarize, if there are no hidden conservation laws, we expect to see points fill an area; if there are hidden conservation laws, we expect to see points fill a curve. What do we see?
Different worlds have been revealed, some fill in closed curves, others fill in areas, yet others carve out islands (the red ones, for example). Interestingly, a fixed point has also been revealed at $(y=0, p_y = -0.25)$. Clearly, some trajectories act as if there are no hidden conservation laws. The dark green one, for instance, fills an enormous amount of area - it acts chaotically; others, however, act as if there is a hidden conservation law - the orange and yellow ones follow a nearly elliptical curve. In extreme cases, we have the peculiar fixed point at $(0, -0.25)$. We have discovered some interesting regularities. If you are like me, you are curious to see what the actual trajectories look like. In the plot below, hold Shift and click on a section point to visualize the trajectory on the right. To clear the selection, double click on the trajectory plot on the right.
A lot of structure has been revealed! We can see that the beautiful triangular trajectory we saw in the beggining correspondts to the brown, orange, yellow islands on one hand, and the light blue islands on the other. What's the difference? The trajectory of the brown-yellow islands goes clockwise whereas the trajectory of the light blue islands is counter-clockwise! Check it out yourself! We can see a smilar relation between the more intricate red and pink islands.
We can also see the second beautiful trajectory we saw in the beggining corresponding to the dark blue island, and we can see its counterpart in the light green island towards the bottom which oscillates from left to right. What about the fixed point at $(0, -0.25)$? It's a perfect case of oscillation from left to right - tracing a straight line in the $x-y$ plane!
Hopefully that has wetted your appetite, we now turn to the rather more challanging Three Body Problem. Specifically, we investigate the Restricted Three Body Problem in which we assume that the third body has negligable mass compared to the other two. Let $a$ be the distance between the two massive bodies. If we set the origin of our coordinate system to be the center-of-mass of the system, the two bodies are: $$a_0 = \frac{M_1}{M_0 + M_1} a \text{ \ \ and \ \ } a_1 = \frac{M_0}{M_0 + M_1} a$$ away from the origin. From Kepler's third law, we can get the oribital frequency of the two bodies around their center-of-mass: $$\Omega^2 a^3 = G (M_0 + M_1)$$ We now define the Lagrangian I used the Lagrangian formulation since it behaves nicer under time-dependent coordinate transformations, such as rotation (something we will need later). of the third body as: In the code to the left, a Lagrangian is a function of a single varible - the local description of the trajectory; i.e. a tuple of (time, position, velocity). The L3rd function constructs a sepcific Lagrangian for a given mass and potential.
def L3rd(m, V):
"""Lagrangian for the third body of mass `m` moving in a
field derived from a time-varying gravitationa potential `V`.
"""
def f(local):
t, q, v = local
return 0.5 * m * v.T @ v - V(t, q)
return f
The Lagrangian of the third body depends on the mass of the third body and a time-varying potential from the two massive bodies. We define the time-varying potential as:
def V(a, GM0, GM1, m):
"""Time-varying gravitational potential for a third body of mass `m`
orbiting two bodies of mass `GM0` and `GM1` with distance b/w them `a`.
"""
Omega = get_Omega(a, GM0, GM1)
a0, a1 = get_a0_a1(a, GM0, GM1)
def f(t, q):
x, y = q
# Get the position of the two bodies at time `t`
x0 = -a0 * jnp.cos(Omega * t)
y0 = -a0 * jnp.sin(Omega * t)
x1 = a1 * jnp.cos(Omega * t)
y1 = a1 * jnp.sin(Omega * t)
# Calculate the distance b/w the third body and the two bodies
r0 = jnp.sqrt((x - x0) ** 2 + (y - y0) ** 2)
r1 = jnp.sqrt((x - x1) ** 2 + (y - y1) ** 2)
# Calculate the potential
return -GM0 * m / r0 - GM1 * m / r1
return f
Remember that in our experiments with the surface of section we used conservation of energy to establish an exact relation, relaying on a hidden conservation law, between the two coordinates of the section (namely $y$ and $p_y$). This allowed us to distinguish trajectories acting as if there is a hidden law (filling a curve described by the relation) from the ones that act chaotically (filling an area). In other words, we need a supplemental conserved quantity to distinguish between the two cases. Unfortunately, for the Three Body Problem in inertial frame there are no known conserved quantities. Fortunately, if we switch to a co-rotating reference frame, there is a known conserved quantity - the Jacobi Integral. An this is what we do. We define our final Lagrangian for the 3rd body to be:
L = compose(L3rd(m, V(a, GM0, GM1, m)), F2C(rotation(Omega)))
for given system parameters a, m, GM0, GM1, where compose is a mathematical composition of two functions, and rotation is defined as:
def rotation(omega):
"""Rotation by `omega`."""
def f(local):
t, [x, y], _ = local
return jnp.array(
[
[jnp.cos(omega * t), -jnp.sin(omega * t)],
[jnp.sin(omega * t), jnp.cos(omega * t)],
]
) @ jnp.array([x, y])
return f
The library used to perform this transformations and others is mechanix - a small library of composable utilities for exploring classical mechanics. Something I built in my free time and was heavily inspired by the amazing scmutils library presented in the book "Structure and Interpretation of Classical Mechanics", by Sussman and Wisdom. and F2C converts a coordinate transformation F (such as rotation) to a local state transformation C which takes into account transforming not only the coordinates, but also the velocities and any higher order components of the local state, accordingly.
Given our final Lagrangian, we can get the energy by using: $$ \begin{align*} \begin{split} \mathcal{E} &= \partial_{\dot q} L \cdot \dot q - L \\ &= \frac{1}{2} m (\dot x^2 + \dot y^2) - m \left(\frac{G M_0}{r_0} + \frac{G M_1}{r_1} + \frac{1}{2} \Omega^2(x^2 + y^2)\right) \end{split} \end{align*} $$ which is succinctly expressed in code by the function transformation:
Contours for the Jacobi integral. The system parameters used for this plot, and the experiments that follow, are: a = 1.0, m = 1.0, GM0 = 1.0, GM1 = GMO * 0.005. GM1 was chosen specifically so we can observe the L4 and L5 Lagrange points. You can see the L4 and L5 points as the inner most orange contours top and bottom accordingly.
def Lagrangian_to_energy(L):
jacL = jax.jacrev(L) # Jacobian of the Lagrangian
P = lambda x: jacL(x)[2] # Partial of the Lagrangian w.r.t.
# the third (index 2) component of the local tuple - i.e. velocity
def f(local):
_, _, v = local
return P(local) @ v - L(local)
return f
The celebrated Jacobi Integral is defined as $C_J = - 2 \mathcal{E}$, therefore:
Energy = Lagrangian_to_energy(L)
Jacobi = lambda local: -2 * Energy(local)
We now construct the Poincaré map (surface of section) for the Three Body Problem. We adopt the same strategy as for the Hénon-Heiles system - recording $(y, p_y)$ whenever $x=0$. Concretely, this is implemented by: In this case, we actually record $(y, \dot y)$; however, $p_y$ and $\dot y$ turn out to be the same in our particular instance of the problem.
def R3BPmap(J, dt, int_eps, sec_eps, *, a, m, GM0, GM1):
sysder = R3BPsysder(a, m, GM0, GM1)
step = state_stepper(sysder, tolerance=int_eps)
def sysmap(qv):
y, ydot = qv
st = section_to_state(J, y, ydot)
cross_st = find_next_crossing(st, dt, step, sec_eps)
y, ydot = cross_st[1][1], cross_st[2][1]
return jnp.array([y, ydot])
return sysmap
where R3BPmap returns the Poincaré map for a given Jacobi Integral value J, time step dt and tolerances int_eps, sec_eps, along with the system parameters. To implement the map, we construct a state_stepper, which takes the system derivative along with the required tolerance and returns a function that performs a single step of Adaptive Runge-Kutta-Fehlberg Method (RKF45). The state derivative is derived from the Lagrangian: To see the full details, checkout the code repository.
def R3BPsysder(a, m, GM0, GM1):
Omega = get_Omega(a, GM0, GM1)
L = compose(L3rd(m, V(a, GM0, GM1, m)), F2C(rotation(Omega)))
return Lagrangian_to_state_derivative(L)
For the mapping itself (sysmap), we first recover the state associated with the current point on the section via section_to_state and then advance this state to the next crossing state via:
def find_next_crossing(st, dt, step, sec_eps):
x = st[1][0]
next_st, dt = step(st, dt)
next_x = next_st[1][0]
while not (x < 0 and next_x > 0):
st, x = next_st, next_x
next_st, dt = step(st, dt)
next_x = next_st[1][0]
return refine_crossing(st, step, sec_eps)
The actual code is a bit more complicated since it uses JAX/XLA primitives for faster computation. You can checkout the details here. Once we find a pair of states between which the $y-p_y$ plane is crossed, the exact crossing state is refined using Newton's method:
def refine_crossing(st, step, sec_eps):
x = st[1][0]
while x > sec_eps:
dx = st[2][0] # velocity in x
st, _ = step(st, -x / dx),
x = st[1][0]
return st
After all this work, what do we get? The section was generated for $C_J = 3.0$. You can brush to zoom and explore the details!
I honestly wasn't expecting to see so much structure in a problem as chaotic as the Three Body Problem. To reveal all this structure, the use of high order accurate numerical method with adaptive step size was essential! I will leave you to explore this curious map yourself, I would only like to empasize the lonely island on the far left of the map, around $(-1, 0)$ - this is the L5 Lagrange point!
In conclusion, we have seen how a simple technique such as surface of section can reveal hidden structure in the dynamics of a system. Obviously, there is a lot more to investigate here. For instance, we have only seen sections for one particular energy level. The question remains how the dynamics of the system changes with energy. Furthermore, I have first-hand observed how the use of high order numerical methods can aid in revealing structure in the surface of section that otherwise is all fuzzy. A promising direction is the exploration of symplectic integration scehemes. I hope you've enjoyed reading this as much as I have enjoyed writing it, and if you have any problems of yours you would like to explore check out mechanix and the awesome "Structure and Interpretation of Classical Mechanics" book by Sussman and Wisdom!